Smith’s Wave Equation Program–the first numerical method

The work of both Isaacs and Glanville et.al. demonstrated two things:

1. Wave propagation in piling was a real phenomenon; predicting it opened up the possibility of accurate prediction of pile stresses and resistance.
2. The mathematical complexity of the problem–related to the complexity of the hammer-cushion-pile system, the existence of shaft friction (which, in theory, forced the use of the Telegrapher’s Equation rather than the undamped wave equation) and the nonlinearities in all parts of the system–made reduction to a relatively simple formula for practical use impossible.

All of these difficulties were recognised by E.A.L. Smith, who ultimately became Raymond Concrete Pile’s chief mechanical engineer. As Graff noted in Raymond’s own publication Foundation Facts:

He (Smith) started to work in the mechanical engineering department, and his first assignment was to try to find out what happened to a pile under driving. He was a skilful mathematician and he spent a number of months on the project, doing a great deal of research. He finally reported that the problem was too complicated to be solved by mathematical means because of the many variables involved. He was able to cite authorities to support his conclusion. Over the years the problem was tucked away in a corner of his mind to be brought out occasionally, re-examined, and then tucked away again. With the development of electronic computers he finally saw the possibility of a solution to the problem. He worked up a general method lo solve impact and longitudinal wave transmission problems in a step by step process…

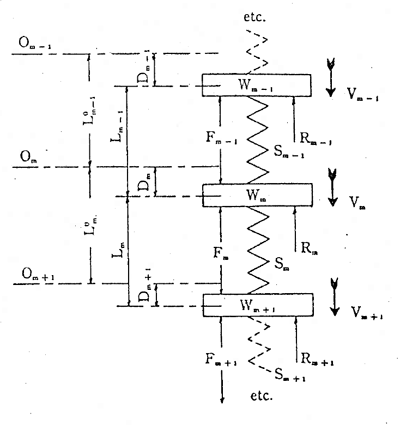
Smith’s first task was to develop a method to analyse the pile. He employed a first-order finite difference technique, dividing the pile into masses and springs. The basics of this were documented in a this monograph, which shows the technique as he set it up at the IBM Technical Computing Bureau. The figure at the right is taken from this monograph; it shows the model schematically, using Smith’s characteristic notation. It was, to my knowledge, the first application of computer simulation to a civil engineering problem.

Using a finite-difference technique (as opposed to a finite element one) was a more sensible solution than it looks to be now, since it avoided the construction of the stiffness matrices the latter technique requires. (“Traditional” dynamic finite element techniques have precision limitations as well, as demonstrated by Deeks and Warrington.) Finite difference techniques have been used elsewhere in pile analysis, most notably with the p-y lateral loading routines developed by Lymon Reese and his colleagues.

His next challenge was to deal with the nonlinearities and inextensibilities in the system. The key nonlinearities were that of the soil and the hammer (and pile) cushion. For the soil Smith first applied an elasto-plastic model, similar in underlying theory to the plastic design techniques used in beams. For the cushion he used a model which he later modified (although it was resurrected independently by Warrington for Vulcan’s ZWAVE program in the 1980’s.)

The inextensibility issue, although overlooked now, was a critical advance, as the “classical” and “closed form” solutions did not directly admit for the fact that the interfaces between the pile cap (or “follower,” using Raymond terminology) and the pile, along with other interfaces, would not transmit tensile forces. It enabled Smith to simply construct the model, set the initial conditions, and let the model simulate the reality of the system without intervention. All of this was discussed in his monograph in the Transactions of the American Society of Mechanical Engineers. Two years later, for the civil engineering profession, he presented a simpler summary of the whole business entitled “What Happens When Hammer Hits Pile” for Engineering News-Record (the same publication which Wellington used to promote his formula seventy years previously.)

After this field tests were in order, and in 1958 the opportunity for one came in Helena, Arkansas, driving both steel pipe pile and the Raymond Step-Taper pile. The Step-Taper pile, a Raymond favourite, was another impetus for the numerical method, as non-constant cross-sections were easily modelled in Smith’s technique.

The various piles used, the soil profile, and the results are summarised below.

As Ernest T. Mosley, who worked in Raymond’s civil engineering department, noted about the results shown above:

These comparisons indicate that for the type of soil encountered at this site and for these types of piles the wave equation solution gives a reasonable good prediction of ultimate pile capacity without the necessity of making modifications for soil freeze or relaxation.

Of the factors used in these wave equation solutions the physical properties of the hammer, capblock and piles are considered to be fairly accurate. However, the soil parameters are known to be not more than reasonable estimates. When more is known of the hammer in which these parameters act under dynamic loading, a more sophisticated wave equation solution can be made. In the meantime wave equation solutions can be usefully employed providing good judgement is used in their interpretation. The results of the case history studies referred to earlier are expected to contribute much toward this end.

Smith’s soil model–ultimately a visco-elastic-plastic model, taking into consideration velocity generated forces along the pile shaft and at the toe–has been subject to some detail improvement, but has endured in its basic concept since Smith set it forth.

Smith’s ASCE paper of the numerical wave equation technique for piling has become one of the classic monographs in the civil engineering profession. As has been the case with many aspects of pile dynamics, it was controversial in some quarters, and it would be another quarter of a century before the wave equation would truly become the “state of the practice” for driven piles. It’s interesting to note that one of the key initial objectors to the technique was Marvin Gates, whose own dynamic formula has become the “standard” of the FHWA. Gates’ main objection was the use of the wave equation for pile capacity prediction, but Smith’s technique has won this argument, as Isaacs predicted thirty years previously.

As Tonis Raamot, Raymond’s chief civil engineer, noted:

The wave equation describes only the structural dynamics of pile driving and does not solve any of the associated soil mechanics problems. It will not predict the length of piles, nor will it predict the long-term behaviour of the soil surrounding the piles. Hence, it does not replace judgement and experience developed by engineers and contractors in the field of pile driving. It merely assists to systematize existing knowledge by accurately describing the energy transfer from the hammer to the tip of the pile. It thus fulfils the function of empirical dynamic pile driving formulas in a much more accurate and comprehensive manner.

Efforts Immediately After Smith

Smith may have seemed to be a hard act to follow, but followed he was. Below are some of the immediate efforts between Smith’s landmark ASCE paper and the TTI/Texas A&M effort.

Pile Driving Analysis Using the Wave Equation

Paul W. Forehand and Joseph L Reese
Princeton University, 1963

The possibility of predicting the ultimate static bearing capacity of a pile from its dynamic behaviour during driving is investigated by the wave equation method of pile driving analysis. The method developed by E.A.L. Smith over a period of years is followed, but its validity is first shown by proving that the mathematical model used is equivalent to the wave equation. Computer programs developed for purposes of this investigation are presented in their entirety together with detailed instructions on their use so that they may be utilised by future investigators who may not be familiar with computer work.

The soil engineering aspects of the problem are explored. The information available on dynamic soil properties from published test data is reviewed to obtain information applicable to pile driving. Using values thus deduced and the computer programs, computations of ultimate resistance are made from 24 published pile driving records and correlated with their load test results.

Although not conclusive because of the relatively small number of correlations attempted, the results are very encouraging. It appears that the wave equation method of pile driving analysis may become an accurate tool in predicting a pile’s static bearing capacity from its driving record. This appears to be the case regardless of the type or size of pile and driving equipment, and indications are that predictions may be possible for piles driven in cohesive as well as granular soils. General limitations of the method are summarised.

Values deduced for point and side damping and ground quake in various soils are presented. Corresponding values of friction acting on the pile sides as a percentage of the ultimate resistance are given for the piles investigated. More research into this problem is indicated, and recommendations are made for such work.

It is concluded that even with inexact knowledge of dynamic soil properties the wave equation method of pile driving analysis appears to give good results.

Evaluation of Pile Bearing Capacity by Use of the Wave Equation

Stuart H. Williams
University of Missouri at Rolla

The wave equation method of evaluating pile bearing capacity is investigated by using data obtained from a comprehensive pile testing program. Modifications which create a more accurate and realistic approach are made to the method proposed by previous investigators. With the use of these modifications, correlation between observed and computed results is more readily obtained.

Selected pile formulas in the empirical, static, and dynamic categories are reviewed so that a direct comparison between these and the wave equation method can be made.