The years after Wellington set forth the Engineering News Formula saw the general acceptance of dynamic formulae as a method of relating the performance of an impact hammer (drop or steam) with the bearing capacity of the pile. The technology of driven piles, however, was not standing still, and two factors in particular began to undermine the relatively homogeneous environment into which Wellington introduced his formula.
The first was the proliferation of the dynamic formulae themselves. Although the Engineering News Formula was the dominant one in the U.S., there were both variations in that formula and other ones which found their way into driven pile specifications. Elsewhere other formulae such as Hiley’s, which took into consideration a wider variety of factors, were more common. The discrepancies amongst the results tended to undermine the credibility of the formulae in general.
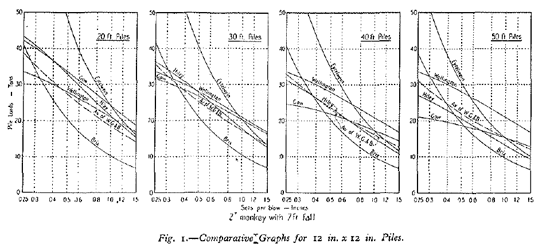
The proliferation of formulae, however, was in part driven by the second factor: the introduction and use of precast concrete piles. As Isaacs pointed out, there were three main differences between wood and concrete piles:
(1) The structural and elastic characteristics of timber piles and concrete piles are very dissimilar.
(2) In drop hammer driving, timber piles. are usually driven direct, with a hammer of weight nearly as great as, or greater than that of the pile; concrete piles are usually driven using a cushion and helmet, and a hammer only a fraction of the weight of the pile.
(3) Concrete piles are relatively more expensive, and a good gauge of their capacity is therefore relatively more valuable.
A more obvious problem was concrete pile damage. Concrete is a brittle substance to begin with, incapable of significant tension, and precast piles lacked the prestress of later concrete piles. Not only was damage being experienced at the head and toe of the piles, but also in the middle of the pile as well, and not always at low sets per blow (high blow counts.) The dynamic formulae had no provision at all to predict pile stresses; in fact, a core part of the theory behind the dynamic formulae was that the pile was a rigid mass. Empirical rules were not effective in predicting the failures that were being experienced.
The solution to this problem was to include the effects of longitudinal wave propagation in piles. The classical one dimensional wave equation is given by the formula
u(x,t)tt = c2 u(x,t)xx
where
- u(x,t) = displacement as a function of distance and time
- c = speed of sound in propagating medium
This equation is a second order, hyperbolic, partial differential equation. It has been solved in one dimension for many years, but most solutions, because of boundary conditions and nonlinearities in an actual hammer-pile-soil system, cannot be directly used with driven piles.
Isaacs’ Work
The first person to apply the wave equation (or stress-wave theory) to model impact pile driving was the Australian David Victor Isaacs with his seminal paper “Concrete Pile Driving Formulae” in 1931. Isaacs started out by reviewing the dynamic formulae. Part of his review included a discussion of the factor of safety, where he makes a statement that is still relevant:
It should be remembered, however, that these are not true factors of safety, but include a “factor of ignorance.” The author suggests that when the ultimate resistance of any pile has been determined, in fixing the factor of safety…the most unfavourable conditions possible in the supporting strata should be judged (the range of conditions possible being narrowed with better knowledge of the subsurface conditions and of the possibility of disturbance from extraneous sources) and a proportion of the factor of safety — a “factor of ignorance” — then allowed in respect to these possible conditions, the manner of determining the ultimate load, and the type of loading to be borne. The remaining proportion of the factor of safety — or true margin of safety — should be approximately constant for all classes of loading and foundation conditions involving the same value of loss in case of failure; and the overall factor of safety…will then be equal to the product of the true factor of safety with the “factor of ignorance.” (p. 305)
After this, he describes an experiment where rods are impacted against each other in a pendulum setup. As the rods were lengthened, the behaviour of the rods deviated more and more from Newtonian impact theory.
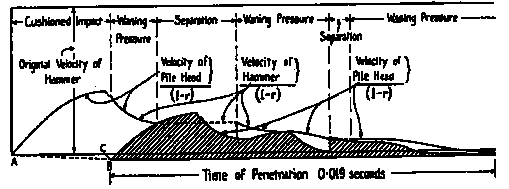 He then went to develop an integration technique that is best described as a semi-graphical one. He developed a mathematical model based on the successive transmission and reflection of waves (similar in principle to the method of images.) A sample solution is given at the right, in this case showing multiple impacts.
He then went to develop an integration technique that is best described as a semi-graphical one. He developed a mathematical model based on the successive transmission and reflection of waves (similar in principle to the method of images.) A sample solution is given at the right, in this case showing multiple impacts.
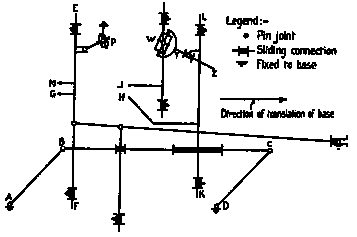 After this he constructed a drafting machine to draw out the solution, a diagram of which is shown at the left.
After this he constructed a drafting machine to draw out the solution, a diagram of which is shown at the left.
He was then able to solve for the stresses and displacements of the pile during driving. Isaacs developed a set of formulae and charts to make his results accessible for the analysis of piles.
In the course of the investigation, Isaacs dealt with a number of questions that would become central to stress wave analysis of piles, including tension stresses in concrete piles, the effect of ram weight (he concluded that to a point a heavier ram reduced tension stresses,) and the effect of cushion material stiffness and drive cap weight.
Isaacs’ work also revealed the computational complexity of stress wave analysis, a complexity that insured the dominance of dynamic formulae in pile analysis (with all of their serious limitations) for another half century.
The Work of Glanville et. al. (1938)
 After Isaacs’ work, the centre of work on the subject shifted to the United Kingdom, with the extensive study commissioned by the British Building Research Board under the direction of (later Sir) W.H. Glanville and his colleagues. This study was one of the first comprehensive studies on stress waves in piles in general. It was occasioned by the problems encountered in the breakage of concrete piles during driving, both at the top and the toe. The wave equation and d’Alembert’s solution were used to develop equations to estimate the stress in the pile during driving, using the method of images. Because of the complexity of the equations, the results were reduced to a series of charts where a quantity of dimensionless stress was plotted against the ratio of hammer weight to pile weight. The charts could then be used to estimate pile stresses and resistance. The charts were applicable to concrete piles only, and this was and is a serious limitation to such solutions, because they were applicable to a limited universe of piles.
After Isaacs’ work, the centre of work on the subject shifted to the United Kingdom, with the extensive study commissioned by the British Building Research Board under the direction of (later Sir) W.H. Glanville and his colleagues. This study was one of the first comprehensive studies on stress waves in piles in general. It was occasioned by the problems encountered in the breakage of concrete piles during driving, both at the top and the toe. The wave equation and d’Alembert’s solution were used to develop equations to estimate the stress in the pile during driving, using the method of images. Because of the complexity of the equations, the results were reduced to a series of charts where a quantity of dimensionless stress was plotted against the ratio of hammer weight to pile weight. The charts could then be used to estimate pile stresses and resistance. The charts were applicable to concrete piles only, and this was and is a serious limitation to such solutions, because they were applicable to a limited universe of piles.

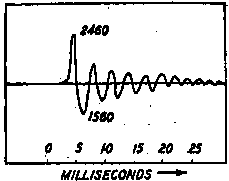
In addition to developing a solution to the wave equation, the authors continued Isaacs’ work in addressing technical issues and experimental techniques that have enduring interest in pile dynamics. These include the instrumentation and data collection on stresses and forces in piles, including remote data gathering through “portable” equipment in a trailer, further research on the effect of the hammer cushion on the generation and effect of the pile stress wave (these were included in the analytical work,) drop tower testing on cushion material to determine the cushion stiffness, and further work on the relationship of ram weight to pile weight and cross section. An example of the data collected is shown above, which shows recorded tension stresses in the midpoint of the pile during driving.
After this study the Second World War interrupted further research; moreover, the difficulties that this study encountered in developing a readily usable prediction technique ended the possibility of using a closed form solution for this application. Although closed form solutions are certainly possible for piles, for practical use a numerical method was necessary, but such a solution would have to wait for the computational power of a digital computer. The wait would not be long.



10 thoughts on “Isaacs and Glanville: The Beginnings of the Wave Equation for Piles”