Billiards and Pile Driving: Newtonian Impact Mechanics and Dynamic Formulae

One thing that many of the “old heads” in this business wish would come back are the dynamic formulae. In some cases they’re still important as they’re written into the codes. So how did they come into being? As noted in my discussion of The Engineering News Formula, and Its Treatment in Early Vulcan Literature, many earlier formulae (including the EN itself) were originally purely empirical. Ultimately, however, the theory behind most of them was Newtonian particle dynamics and conservation of momentum, the same theory as you use to play billiards or pool. The presentation we’ll use of the basic theory is Seely, F.B., and Ensign, N.E. (1921) Analytical Mechanics for Engineers, published by John Wiley & Sons, New York, NY. Fred Seely was a well known author of textbooks on this and related subjects and his name is doubtless familiar to older engineers.

Pile driving is simpler than pool in one important aspect: it takes place in one dimension (assuming, of course, the hammer and pile are properly lined up.) Since momentum (the product of force and time, or mass and velocity) is a vector quantity, this simplifies the math considerably. The following diagram illustrates two masses with two velocities approaching impact, in this case the motion is horizontal rather than the vertical motion we associate with pile driving:

The variables we’ll use are as follows, we’ll add a few more as we go along:

The conservation of momentum going into, through, and coming out of impact are as follows:

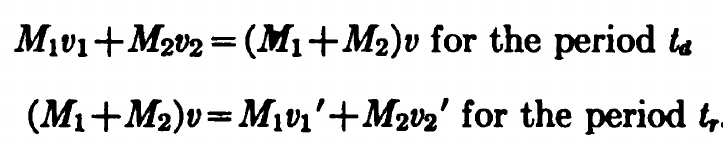
We define the coefficient of restitution as follows:

The relationship between this coefficient of restitution and the one used for a cushion material in the wave equation analysis is discussed in my post A Tale of Two Coefficients of Restitution. It is an indication of the efficiency of impact. When e = 1, the impact is perfectly efficient and both bodies come out with different velocities. When e = 0, it is perfectly inefficient, the bodies basically go “splat” and come out as one with one velocity. A value of e = 1 is virtually impossible in the physical world; a value of e = 0 is possible if one body becomes embedded in another. In this case the hammer velocities are v₁ and v’₁ and the pile velocities are v₂ and v’₂.

For convenience we should also define the mass (or weight) ratio between the impact ram and the pile, thus

I.n any case, if we put these into matrix form, we get the following:

Inverting the matrix and solving for the velocities after impact, we have

Let us define the stroke speed coefficient R as

Then

This expression lines up with that given in Russian Impact-Vibration Pile Driving Equipment: Chapter 2, Theory of Operation. It is worth noting that the Soviets, for all of their mathematical prowess, never implemented wave theory in pile driving in a comprehensive way, but mostly stuck with the mechanics described in this article.

If we assume (as is normal) that the initial pile velocity at impact v₂ = 0, then

We can plot this result as a function of m’ and e below.

Based on this, we can say the following:

• The negative values of R are not a mistake; they indicate that, in those cases, the ram velocity is negative after impact, i.e. upward. This means that energy has rebounded back to the ram. Generally speaking, in calculations such as Checking the Soviets: Finding the Frequency and Establishing Basic Parameters, the stroke speed coefficient is taken as the absolute value of the velocity ratio.
• As one would expect, the greatest rebound velocities to the ram take place when a) the pile is the heaviest and b) the coefficient of restitution is its highest (at unity.) This fact explains why pile to ram weight ratios were traditionally limited. With lower pile weights more energy was believed to have gone to the pile.

Hammer manufacturers use rebound differently depending upon the type of hammer and the application. Vulcan air/steam hammers were always designed to operate with no rebound. The hammers described in Soviet S-834 Impact-Vibration Hammer: Calculations, Part I used a value of R = -0.12 and sometimes up to R = -0.20 (using the definition of R above.) Diesel hammers require a great deal of rebound to run, which is evidenced by the difficulties they have in very soft soils.

Of greater interest to geotechnical engineers is the velocity of the pile after impact. We can represent this by the following ratio:

If we apply the above result and assume again that v₂ = 0, we get this result for S:

It’s worth noting that, for e = 0, the two stick together and move with the same velocity after impact. It’s also worth noting that, for light piles, it’s possible that the pile will move faster than the ram after impact, which one can see in very soft soils.

So can we move forward with what we have here, either for hammer design or for drivability estimates? The answer is “not really” for the following reasons:

• The physics described above is for particle dynamics, and while the ram can be described as a “particle” in some cases the pile cannot. This relates to wave transmission in the pile; the pile doesn’t “feel” the impact in one instant but progressively as the wave goes down the pile. There is also no way to compute pile stresses here, a weakness which was exposed with the advent of concrete piles and became the genesis of wave mechanics in piles as discussed in Isaacs and Glanville: The Beginnings of the Wave Equation for Piles.
• The value of e is very problematic. The interaction of ram, cushion material, driving accessory and pile head is a complex business, one which these simple Newtonian impact mechanics cannot replicate
• It can be shown that, even if the pile is infinite in length (and weight/mass) the rebound will be much less than shown above. This is evident in the monographs OTC 5395 Revisited: Analysis of Cushioned Pile Hammers and Concrete Pile Head Response to Impact.

So, while this theory was a start for pile dynamics, it certainly was not the end.