It didn’t take long for designers and builders of civil works to realise that the Sanders Formula had significant limitations. The obvious solution at the time (and later when other formulas were found to have feet of clay) was to produce new dynamic formulae. In the twenty years after the end of the Civil War, the main competitor to Sanders was the Trautwine Formula. Although it had variations, the basic format was the following:

The Trautwines were one of the most prominent families in American civil engineering, and the formula was put forth by the junior John C. Trautwine. There were two major steps forward from Sanders in the formula’s structure:
- The cube root of the drop height was used. Sanders had assumed that the penetration of the pile was directly proportional to the energy output of the hammer. Trautwine’s formula penalised hammers with long strokes and light ram weights.
- Trautwine added an additive constant to the denominator, which prevented the pile load capacity from going to infinity with zero. This solved the most immediate weakness of Sander’s Formula from a use standpoint.
However, the 29 December 1888 edition of Engineering News would change everything. Arthur Mellen Wellington, another prominent American civil engineer, published a formula that would dominate pile dynamics (in the US, at least) for the next eighty years, the Engineering News Formula. Although it has many variations (some published in the original article) its basic form was and is as follows:

where
- L = safe load
- F = “constant determined from experience”
- w = ram weight
- h = drop height of ram (assumes single acting hammer)
- s = penetration of pile per blow
- c = “some constant in addition to s”
In 1893 Wellington put together a compendium of articles on the origin and his subsequent defence of the EN formula. Some of the content of this from the standpoint of using the formula were summarised in Vulcan’s product literature, as shown below. Following are some observations about the formula and how it came into being:
- The Engineering News formula was largely an empirically developed formula. Although later engineers would show that it could be developed from Newtonian impact mechanics, there is no indication that Wellington did so at the time. The factors used (except, obviously, for the weight, drop height, and pile set) were also empirical.
- Wellington’s main objective with the EN formula was to displace the Trautwine formula; in fact, the original article was in response to a letter from John C. Trautwine Jr.
- Wellington adopted Trautwine’s addition of the additive constant in the denominator. Wellington attrributed this to the inertia of the pile during impact.
- The EN Formula, as with Sanders, assumed that the penetration of the pile was linearly proportional to the rated striking energy of the hammer, be it drop or steam operated. This was important to Wellington, and he touted it as a major advantage over Trautwine’s cube root of the stroke (and thus the energy.) Unfortunately Wellington’s insistence of this overlooks the fact that, for the same energy, the impulse of the impact decreases with a longer stroke and a lighter ram, which changes the character of the blow. (This issue appears again and again in pile driving, as can be seen here.) It’s intersting to note that the Gates Formula, the formula currently favoured by the FHWA, uses the square root of the energy.
- As formulated by Wellington, the EN Formula has a factor of safety of six. Although useage of the term wasn’t as precise then as now, the intent of the factor of safety was to produce a load that could be used an applied load of the structure the pile supported. More current usage further reduces the result of the EN Formula by another factor of safety, but that wasn’t the original concept.
- Wellington used many “job site examples” to buttress his contention that the EN Formula was an improvement over Trautwine and the other formulas in use at the time. His presentation strikes us as vague and unscientific, but that observation should be tempered by a few considerations:
- Soil mechanics was still very much in its infancy in this “pre-Terzaghi” era. There were no methods of estimating the pile capacity based on soil properties, which would have been a good check on all of the dynamic formulae. Phenomenon such as soil freeze and relaxation were not well quantified, either.
- Wellington (and everyone else) set forth a good deal of load testing data. There were, at time time, no accepted standards for either conducting load tests or interpreting the data, and would not be for some time (the Davisson Criterion, for example, would not come into being until the 1970’s.) Comparing load testing data was very much an “apples and oranges” proposition; load tests were conducted with an eye on the specific job, not on a standard test procedure.
- There was no way to instrument the piles during driving, and would not be until Glanville et. al. in the 1930’s.
Wellington was an energetic and supremely self-confident evangelist of his formula. In one particularly enthusiastic passage, he characterises some of his fellow engineers in New Testament terms:
In so very uncertain a matter it is wrong in principle to start from high ultimates which are certainly unsafe as a unit, and allow foolish men to deceive themselves with the notion that they are being cautious when they divide it by three or. four, when they are really running great risks. The carnal mind longs for this comforting assurance, but the true formula for piledriving is one which is certainly safe in any kind of uniform material, leaving the engineer to realize that he is running risks (which yet may be justified and reduced by caution), if in special cases he goes beyond it.
This notwithstanding, Wellington was a realist about the value of this or any other formula, and set forth conditions under which it could be relied upon (see below.) Wellington himself stated that “…piledriving and pile loading must forever remain an empirical art, defying close analysis by formula,” which should give pause to anyone blindly using the EN Formula (it’s not a good idea for any other geotechnical engineering design method, subsequent advances notwithstanding.)
Wellington’s vigourous promotion of his formula doubtless contributed to its early and widespread acceptance (a course that was repeated by George Goble in the 1970’s with the wave equation based methods.) But how well does the EN Formula actuall predict pile capacity?
Part of the answer, of course, depends upon one’s definition of “pile capacity,” which, as we have seen, wasn’t as well standardised in Wellington’s day as ours. Beyond that, studies have varied in their results. Some have reported reasonable agreement with the wave equation, while others have characterised the EN Formula as unreliable from a statistical standpoint. As long as the majority of driven piles were wood (relatively short) and geotechnical design remained a conservatively practiced art, the weaknesses of the EN and other dynamic formulae could be overlooked. But as both the technology of driven piles and the desire for greater precision and economy progressed, the shortcomings of the EN Formula became more apparent.
Vulcan and the Engineering News Formula
Although Vulcan’s “heavy ram and low striking velocity” philosophy of steam hammer design would favour a formula such as Trautwine’s or Gates’ over the EN, nevertheless Vulcan included extensive information on the formula in its literature for most of the twentieth century. It’s interesting to note that the “Warrington-Vulcan” single-acting hammer line came into existence around the time the EN was set forth, and Wellington used different constants for steam hammers. The narrative below appeared, with small modifications, from 1906 to 1931 (this particular one is taken from the 1914 catalogue.)
Safe Bearing Load for Piles
Numerous formulas have been devised for the bearing power of piles, but their several results have been conflicting and have frequently failed when tested by practice. Engineers, therefore, use them with caution.
It is held by Hering and others that, in order to be reliable, a formula should involve the set of the pile under the last blow: and, furthermore, this blow shold be given after an interval of rest.
For the convenience of our customers we give below the formula devised by the late A.M. Wellington, and originally known as the “Engineering News” formula. It is reproduced from the treatise on “Piles and Pile Driving,” published by the Engineering New Publishing Co., of New York.
The formula may be expressed in the form of a rule, as follows:For Drop Hammers
To find the safe load, in pounds, multiply twice the weight of the hammer in pounds by its fall in feet and divide by the set, in inches, under the last blow, plus one inch.
Concerning this constand, 1 inch, Wellington wrote in reference to Steam Hammers:” * * * The constant 1 (in the formula for Drop Hammers) * * * which represents the extra initial resistance of getting the pile into motion again, should not be over 1/10 as great, if so much.” Therefore,
For Steam Hammers
take the weight of striking parts, in pounds, instead of hammer, in rule above, and in the divisor use 1/10 instead of 1 inch.
The assumed factor of safety is 6.The formula is to be applied subject to the following limiting conditions:
The leader guides must be truly vertical and in good working order.
“The full fall must only be counted (1) when there is no sensible bounce after the blow, and (2) when the head of the pile is in good condition. * * * A broomed head will destroy from half to three-quarters of the effect of the blow, even in the brooming be only a half inch to an inch deep. * * * The remedy is to adze or saw off the heads before giving the last blows * * *
“The proper value of s can only be determined by taking the mean of the sets for a number of blows–nor then, unless (a) the penetration has been at a reasonably uniform or uniformly decreasing rate, and (b) there is reasonable assurance that the penetration wold continue uniform if driven several feet further, * * * and d) the penetration must be at a reasonably quick, as well as uniform, rate–not less than 1/4 inch for a 3000-lb. hammer falling 30 feet.
“There is nearly always an increase of resistance and a decrease of set per blow as an effect of an interval of rest, permitting the earth to settle around the pile. * * * and the mean penetration for the first few blows, after such an interval of rest, should be taken as the valve of s (set of pile in inches.)”
Illustration
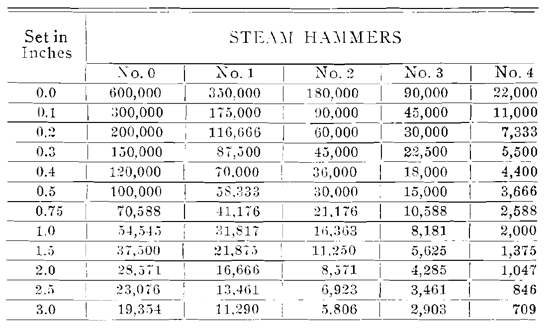
Assume a No. 2 steam hammer and the pile to have been driven a foot in the last ten blows, the weight of the striking parts is 3000 pounds and the fall about 3 feet. The mean set is 12 inches divided by 10, or 1 2/10 inches. Substituting numerical values in the formula, we have
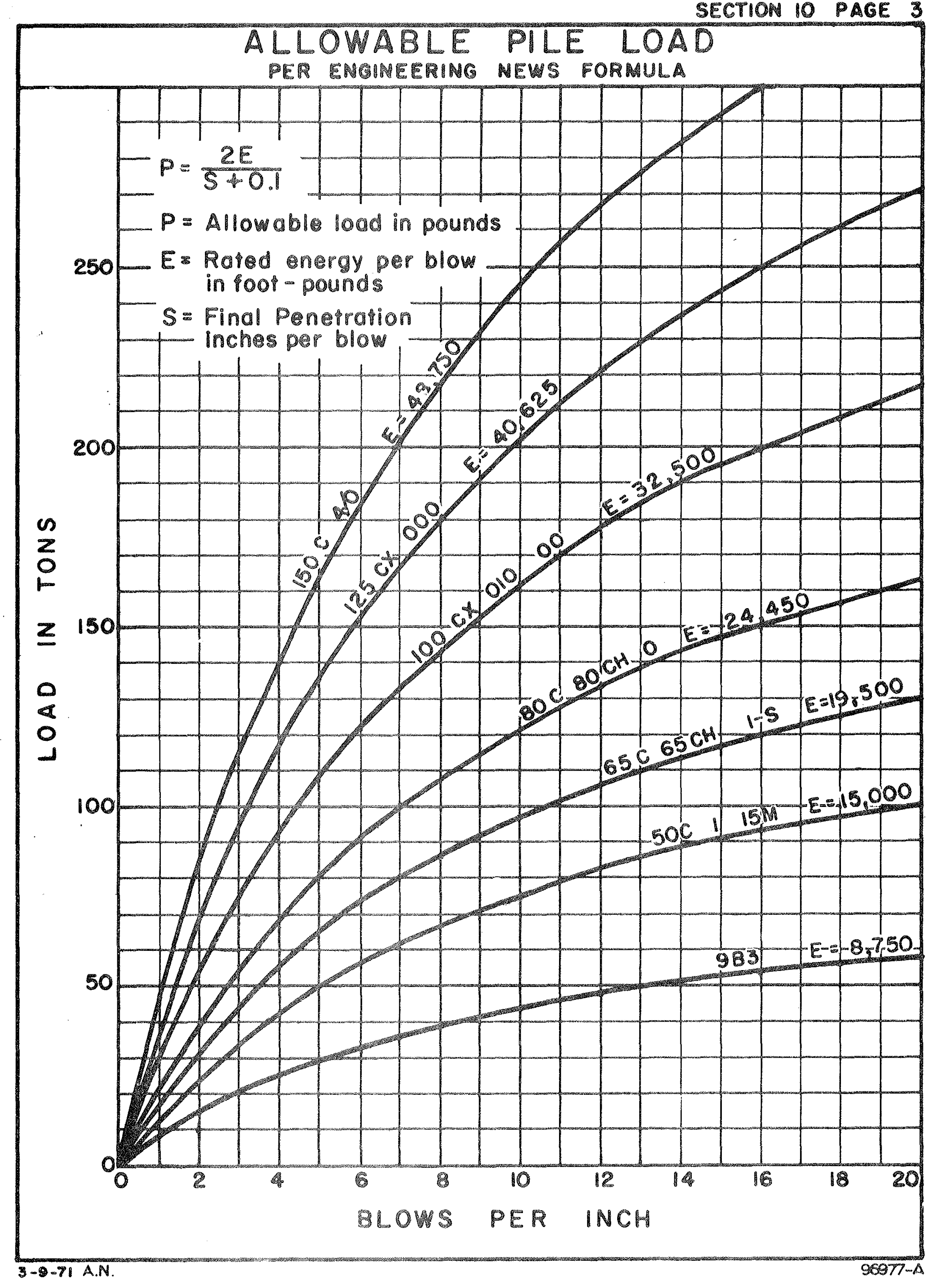
The table below gives the safe load for a pile driven by a steam hammer and using the above formula:Safe Bearing Load for Pile in Pounds
Force of BlowWe are often asked to give the force of the blow of our steam hammers. This depends upon the set and elastic compression of the pile under the blow; therefore no general answer can be given.
It may be well to state that the ram falls by gravity. Then, for both drop and steam hammers, the energy of the blow, usually expressed in foot-pounds, is the product of the weight of ram multiplied by its fall. The useful work in foot-pounds done upon the pile is the product of the resistance of the pile multiplied by its set under the blow. The ratio of these two quantities is the efficiency of the blow. This efficiency depends upon the proportion of work wasted. Work is wasted by bruising and shattering the pile; by the elastic rebound of the ram; by producing vibrations in the pile: by generating heat, and possibly in other ways. The waste of work is greater the higher the velocity of ram at impact. Therefore, heavy rams with low fall give blows of higher efficiency than light rams with a high fall. This explains in part the superior efficiency of the steam hammer, the other factor being the rapid succession of the blows.
Concerning the relative efficiency of blow of steam and drop-hammers, we are without exact experimental results, but a comparison may be drawn from the data contained in the following letter from the Wilcoxon & Kearns Co.:
Pensacola, Fla., Jan. 18, 1900
Vulcan Iron Works, Chicago,
Gentlemen: We have just finished a contest between the old-fashioned drop hammers and one of your No. 1 steam hammers, which no doubt will interest you. We are at present engaged in the construction of a large wharf and warehouse for the L. & N. R. R. at Pensacola, Fla., which requires seven thousand piles from sixty eighty feet long. When we began driving here the chief engineer, superintendent of bridges and resident engineer had never seen a steam hammer work, and, of course, were a little afraid to risk it without a test of the drop hammer being first given. As the piles that had been driven had practically no broomage, the superintendent of bridges concluded that they had not given the resistance necessary to secure a good foundation. To satisfy him we changed the steam hammer for a 4,200-lb. drop hammer and started on a pile (half driven with the steam hammer) with a hood weighing 1,000 lbs. with a life oak cushion block. The hammer had a drop of 60 feet and the pile only showed 1 1/4 inch penetration to each blow. It completely mashed the live oak cushion block into pulp. We then drove a pile 75 feet long with the drop hammer, without the hood, which took 50 minutes time after it was in the leads, and required 120 blows from the top of 75-foot leaders. On the next pile, the same length, 3 feet from the one driven, we used the steam hammer and drove it the same depth with 130 blows, in 90 seconds after it was in the leaders. This pile had no broomage, while the one alongside of it, driven with the drop hammer without a hood, was broomed over three feet. The piles are creosoted piles and cost forty cents per food net, delivered at the work. This would make a saving of 21,000 feet of piling on this job, at forty cents per foot, amounting to $8.400.*
* * * * * * *Yours truly,
WILCOXON & KEARNS CO.For the No. 1 steam hammer the energy of the blow is 5000 lbs. (weight of striking part) multiplied by 3 1/2 (its fall in feet), or 17,500 ft-pounds.**
For the drop hammer the energy of the blow is 4200 lbs. multiplied by 60 feet, for 252, 000 ft-pounds.
The ratio is 1 to 14.4; therefore the efficiency of the blow of the steam hammer is, in this particular instance, 14.4 times that of the drop hammer. This value would indicate that the constant in the divisor of Wellington’s formula should be less than he gives, viz.: 0.1: but it is not safe to generalize from one example.
Notes:
- For a comparison of money values from the first part of the twentieth century to the first part of this one in both the US and UK, take a look at the appendix to this.
- Stroke for later Vulcan #1 hammers is 3′. This is probably due to raising the nominal impact point of the ram. Same comment applies to the #2 example above.
Vulcan’s later literature had more elaborate charts and verbiage on the subject of the Engineering News Formula, and of course was included in literature on the differential-acting hammers when they were introduced in the late 1920’s. EN information was never included in offshore literature, and was dropped from all Vulcan literature in the 1970’s.


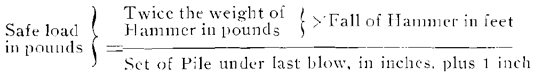
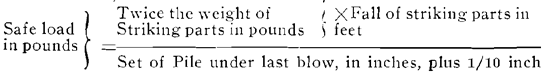
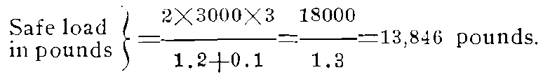

13 thoughts on “The Engineering News Formula, and Its Treatment in Early Vulcan Literature”