How the Saximeter Works, and Why You Can’t Use It on a Vulcan (or any other External Combustion) Hammer

One interesting device people use to estimate the output energy of a diesel hammer is the Saximeter. Originally developed by Pileco, it’s a quick way to estimate the output energy based on the blow rate of the hammer.

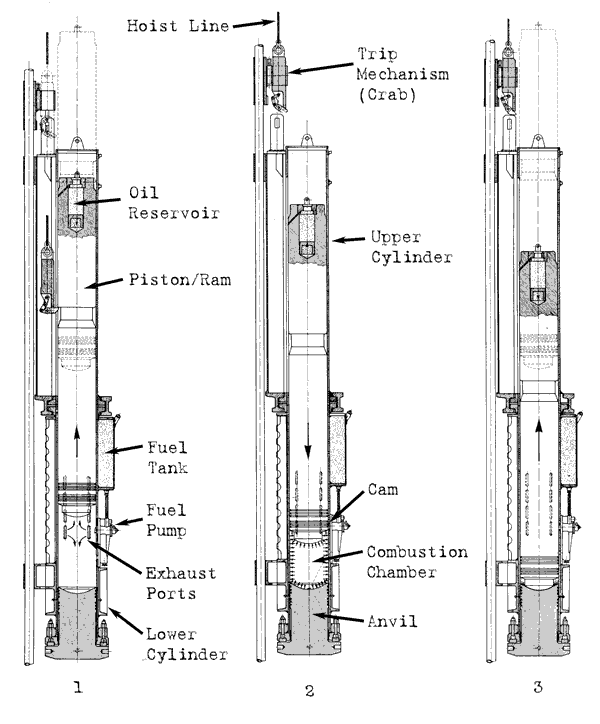
The Saximeter takes advantage of the fact that the diesel ram (of a single-acting diesel at least) spends most of its flight in either free rise or free fall, allowing for the friction of the rings and the back pressure of the exhaust ports. The combustion chamber exerts its upward explosion and expansion pressure on the ram in a relatively short distance. (The chamber also exerts upward pressure during downstroke and compression, which effects its output energy, but that’s another post…)

Following is an overview of the math behind the Saximeter. A more complete derivation is at the end of the post.

If we assume that the ram is acting as if it is in a vacuum, the relationship between the stroke of the ram and the time it takes to fall from topstroke to impact is

(1)

where

• ram stroke, ft. or m.
• acceleration due to gravity = 32.2 ft/sec² or 9.8 m/sec².
• upstroke or downstroke time, sec.

Since the ram makes a full “round trip,” the total time is twice that of the upstroke (or downstroke) time, or

(2)

where = total cycle time, seconds.

Substituting,

(3)

Diesel hammers, like most anything else, don’t operate in a vacuum, and early a correction was made for things such as the combustion chamber, ring friction, backpressure, etc. Using the rule of thumb of 100 mm (0.3′) for the correction, the Saximeter equation can be stated this:

(4a, U.S. Units, h in feet)
(4b, SI Units, h in metres)

It’s possible to measure the blow period (time between blows) using a camera. In that case you can time several blows and divide the total time by the the number of blow periods. Thus, if you start with Blow 1 and stop at Blow 11, you have ten blow periods. But the Saximeter has convenience features which make the job easier (including embedding the correction factors.)

Why This Doesn’t Apply to Vulcan (and any Other External Combustion) Hammer

It would be nice if this convenient way of estimating the rated energy of a single-acting diesel hammers could be applied to, say the Warrington-Vulcan or Super-Vulcan hammers. But it can’t, and that prohibition applies to any external combustion hammer, including (and especially) the hydraulic hammers.

As is evident above, an important assumption for the Saximeter principle to work is that the transfer of energy from pressurised fluid to ram on the upstroke be, for practical purposes, instantaneous. With the possible exception of the Single-Compound hammer, that’s not the case with external combustion hammers. The pressure to move the ram upward is exerted over a significant portion of the upstroke. Vulcan hammers traditionally used around half the upstroke to get the ram to the top, but that’s not consistently true, and with the Raymond hammers it sometimes gets to around 75% of the upstroke. (The downstroke is unopposed by compressed air or steam until just before impact, similar to a diesel hammer.) So the timing assumption of the Saximeter principle doesn’t apply.

This is even more true with hammers that have downward assist. Most hydraulic hammers, the MKT “B” and “C” hammers, the California series of hammers, the DGH hammers and of course the Super-Vulcan hammers fall in this category. Vulcan walked into this trap with this correlation, from the 1938 literature for the closed-type Super-Vulcan hammers:

Although GRLWEAP recommends using 50% mechanical efficiency for Super-Vulcan hammers, the 80-85% figure is not unreasonable if the hammer is properly lubricated and maintained. That of course is the problem: the glory of Vulcan hammers is that they will run with minimal maintenance, but their efficiencies suffer. (A diesel hammer either runs properly lubricated or doesn’t run at all.)

It’s interesting to note that Vulcan stated that “The relationship indicated therein holds true only for small sets per blow.” It was Vulcan’s assumption that the longer impact time of lower blow count driving would affect these results, but that was the least of their problems. The greatest problem was rebound. Vulcan hammers are designed to operate with no rebound from the pile (diesel hammers require it, which is why they are hard to start in soft soils.) As rebound energy increased, the operator cut back on the pressure to prevent overstroking, thus decreasing the energy (as was predicted by the third paragraph.)

This created no end of problems for Vulcan until it retracted correlations like this and went strictly to a pressure relationship, such as this table taken from Vulcan’s Data Manual.

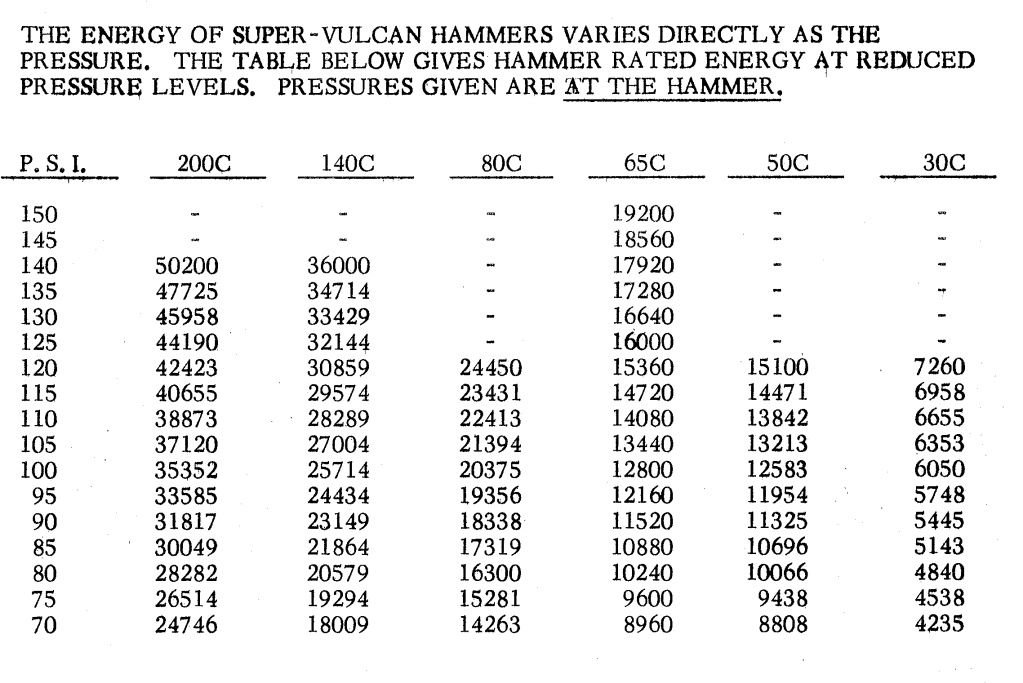
Even with this, the need to reduce pressure with rebound complicated things, which is one reason why the Super-Vulcan hammers, for their elevated blow rate, never displaced their single-acting Warrington-Vulcan counterparts.

Derivation of the Saximeter Equations

The following is a purely theoretical derivation of the Saximeter equations. It assumes no resistance to the ram due to friction, back pressure, or effects due to the distance the ram travels through the combustion chamber. As you saw above, there are corrections for these factors.

The basic equation of motion for an object with a constant downward force acting upon it (in this case gravity) is

(5)

where m is the mass of the object, x(t) is the displacement of the object as a function of time (t), and W is the downward force.

If W is the weight of the ram (external force being gravity,) this simplifies to

(6)

where gc is the gravitation acceleration constant (given above.)

Integrating,

(7)

Setting the velocity at t=0 to v₀ (initial velocity) yields

(8)

Integrating again,

(9)

Again setting the position of the ram at t=0 to x₀ (initial position,) we have

(10);

Differentiating,

(11)

The time from t=0 to the top of the stroke (where the velocity is zero) can be solved to

(12)

Customarily with pile driving equipment the “zero point” of displacement is the impact point, or x₀ = 0. Substituting t_up in Equation (12) into the time in Equation (10), we solve to obtain the maximum height of the ram or the stroke s,

(13)

from which

(14)

This means that the initial velocity of the ram and the stroke have a one-to-one relationship. Substituting the result of Equation (14) into Equation (10) (along with assuming x₀ = 0) and setting x(t) = 0 (the impact point) yields

(15)

Now we can solve (using the quadratic equation) the time(s) at which the ram comes to the impact point. These are

(16)

It is tempting to characterise the first result as the “trivial solution.” It is not; it is simply the starting time of the hammer cycle. The second result is thus the end time. If we solve the second result for the stroke, we have at last

(17)

This is identical to the result of Equation (3). The thing that makes the Saximeter work is that the diesel hammer’s displacement-time history for the upstroke is essentially the mirror image for that of the downstroke, which, as discussed earlier, is not the case for external combustion hammers.