Estimating the Starting Time of a Vulcan Vibratory Hammer

The 1400, driving sheeting for a creosote plant environmental remediation in Chattanooga. The 1400 incorporated many of the features of the 400, including the curved eccentric case (which was mated to the 7″ clamp.) The original suspension was an H-beam, but this proved too light for bias weight, and was replaced by the cast unit shown.

Most of the attention to the way vibratory hammers start and stop is focused on the effect it has on the suspension and the crane boom. A good suspension system (such as the one shown at the right) will dampen most of these vibrations even during start-up, when the lower rotational frequencies run through the resonant frequency of the suspension on their was to the operating frequency of the driver. This analysis will concentrate on the effect of the mass moment of inertia of the eccentrics on the length of time it takes for the eccentrics to come up to speed.

The basic physics is simple: the motor applies a torque to the eccentric, whose speed progressively increases until the maximum flow of the power pack determines the operating speed of the driver. We will consider the 1400, which has the additional simplifying advantage of the motor directly driving one of the eccentrics at the same speed as the eccentrics rotate, that eccentric in turn driving the other. We will assume that there are no mechanical losses in the system (bearing friction, gear losses, losses due to the churning of the oil, etc.) and that the case is fixed. Doing this reduces the basic equation of motion to

${\it I_o}\,{\frac {d^{2}}{d{t}^{2}}}\theta(t)=T$ (1)

where

I_o = mass moment of inertia of the eccentrics, slug-ft2
t = time, seconds
T = torque, ft-lbs
θ(t) = angle of eccentrics as a function of time

Setting the initial velocity to zero and integrating,

$\left ({\frac {d}{dt}}\theta(t)\right ){\it I_o}=Tt$ (2)

Since

${\frac {d}{dt}}\theta(t) = \omega$ (3)

we substitute and obtain

${\it I_o}\,\omega=Tt$ (4)

Solving for time,

$t = {\frac {{\it Io}\,\omega}{T}}$ (5)

Equation (5) gives us the time to come from rest to a given rotational speed with a given torque and mass moment of inertia. The parameters are as follows:

I_o = 4.59 slug-ft²
ω = 251.33 rad/sec (2400 RPM)
T = 4170 ft-lbs (from manufacturer’s data at 2500 psi operating pressure)

Substituting these into Equation (5) yields t_start = 277 msec. Anyone familiar with this type of equipment knows that this is too short, that we should expect a start-up time of around 3-5 seconds. So what gives?

The assumption that the case is fixed may be part of the problem; the fact that the case resists the motion of the eccentrics, especially at the lower speeds, is certainly an issue. A more serious issue, however, is the torque assumption. The output torque of a hydraulic motor is a function of its input pressure, but in reality it’s a function of the difference in pressures between the input pressure (supply) and output pressure (return.) The return pressure of these motors of these systems can be considerable, especially when combining 100′ of hose with a quick disconnect at the power pack. Also significant is the fact that this is the starting pressure; there may be significant delay in getting the full starting pressure to the motor due to the same 100′ of hose.

Below is a chart of Equation (5) with the starting time varied from 10% of maximum torque (250 psi difference across the ports) to full torque (2500 psi difference across the ports.)

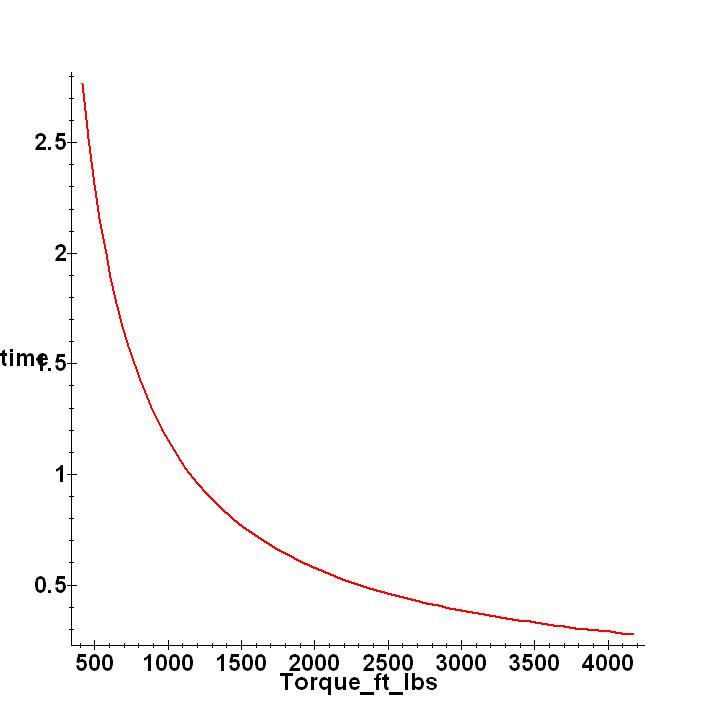
It is easy to see that the starting time can be considerably longer in the lower pressure differentials between the motor ports.

This problem is a good illustration of the basic physics behind vibratory eccentrics, and how assumptions can affect the outcome of engineering calculations. Although most emphasis is placed on the eccentric moment, the mass moment of inertia is an important quantity. Its impact on vibratory driving through its effect on the rotational frequency of the machines is discussed in depth in one of the Two Papers on Vibratory and Impact-Vibration Hammers (actually both) linked to here.